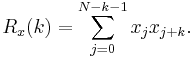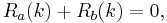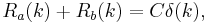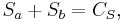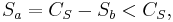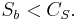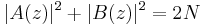Complementary sequences
- For complementary sequences in biology, see complementarity (molecular biology).
In applied mathematics, complementary sequences (CS) are pairs of sequences with the useful property that their out-of-phase aperiodic autocorrelation coefficients sum to zero. Binary complementary sequences were first introduced by Marcel J. E. Golay in 1949. In 1961–1962 Golay gave several methods for constructing sequences of length 2N and gave examples of complementary sequences of lengths 10 and 26. In 1974 R. J. Turyn gave a method for constructing sequences of length mn from sequences of lengths m and n which allows the construction of sequences of any length of the form 2N10K26M.
Later the theory of complementary sequences was generalized by other authors to polyphase complementary sequences, multilevel complementary sequences, and arbitrary complex complementary sequences. Complementary sets have also been considered; these can contain more than two sequences.
Contents |
Definition
Let (a0, a1, ..., aN − 1) and (b0, b1, ..., bN − 1) be a pair of bipolar sequences, meaning that a(k) and b(k) have values +1 or −1. Let the aperiodic autocorrelation function of the sequence x be defined by
Then the pair of sequences a and b is complementary if:
for k = 1, ..., N − 1.
Or using Kronecker delta we can write:
where C is a constant.
So we can say that the sum of autocorrelation functions of complementary sequences is a delta function which is an ideal autocorrelations for many applications like radar pulse compression and spread spectrum telecommunications.
Examples
- As the simplest example we have sequences of length 2: (+1, +1) and (+1, −1). Their autocorrelation functions are (2, 1) and (2, −1), which add up to (4, 0).
- As the next example (sequences of length 4), we have (+1, +1, +1, −1) and (+1, +1, −1, +1). Their autocorrelation functions are (4, 1, 0, −1) and (4, −1, 0, 1), which add up to (8, 0, 0, 0).
- One example of length 8 is (+1, +1, +1, −1, +1, +1, −1, +1) and (+1, +1, +1, −1, −1, −1, +1, −1). Their autocorrelation functions are (8, −1, 0, 3, 0, 1, 0, 1) and (8, 1, 0, −3, 0, −1, 0, −1).
- An example of length 10 given by Golay is (+1, +1, −1, +1, −1, +1, −1, −1, +1, +1) and (+1, +1, −1, +1, +1, +1, +1, +1, −1, −1). Their autocorrelation functions are (10, 1, 2, 3, −2, −1, 0, −1, 0, 1) and (10, −1, −2, −3, 2, 1, 0, 1, 0, −1).
Properties of complementary pairs of sequences
- Complementary sequences have complementary spectra. As the autocorrelation function and the power spectra form a Fourier pair complementary sequences also have complementary spectra. But as the Fourier transform of a delta function is a constant we can write
- where CS is a constant.
- Sa and Sb are defined as a squared magnitude of the Fourier transform of the sequences. The Fourier transform can be a direct DFT of the sequences, it can be a DFT of zero padded sequences or it can be a continuous Fourier transform of the sequences which is equivalent to the Z transform for Z = ejω.
- CS spectra is upper bounded. As Sa and Sb are non-negative values we can write
- also
- If any of the sequences of the CS pair is inverted (multiplied by −1) they remain complementary. More generally if any of the sequences is multiplied by ejφ they remain complementary;
- If any of the sequences is reverted (inverted in time) they remain complemantary;
- If any of the sequences is delayed they remain complementary;
- If the sequences are interchanged they remain complementary;
- If both sequences are multiplied by the same constant (real or complex) they remain complementary;
- If both sequences are decimated in time by K they remain complementary. More precisely if from a complementary pair ((a(k), b(k)) we form a new pair (a(Nk), b(N*k)) with zero samples in between then the new sequences are complementary.
- If alternating bits of both sequences are inverted they remain complementary. In general for arbitrary complex sequences if both sequences are multiplied by ejπkn/N (where k is a constant and n is the time index) they remain complementary
- A new pair of complementary sequences can be formed as [a b] and [a −b] where [..] denotes concatenation and a and b are a pair of CS;
- A new pair of sequences can be formed as {a b} and {a −b} where {..} denotes interleaving of sequences.
- A new pair of sequences can be formed as a + b and a − b.
Golay pair
A complementary pair a, b may be encoded as polynomials A(z) = a(0) + a(1)z + ... + a(N − 1)zN−1 and similarly for B(z). The complementarity property of the sequences is equivalent to the condition
for all z on the unit circle, that is, |z| = 1. If so, A and B form a Golay pair of polynomials. Examples include the Shapiro polynomials, which give rise to complementary sequences of length a power of 2.
Applications of complementary sequences
- Multislit spectrometry
- Ultrasound measurements
- Acoustic measurements
- radar pulse compression
- Wi-Fi networks,
- 3G CDMA wireless networks
- OFDM communication systems
- Train wheel detection systems
- Non-destructive tests (NDT)
- Communications
See also
- Pseudorandom binary sequences (also called maximum length sequences or M-sequences)
- Gold sequences
- Kasami sequences
- Walsh–Hadamard sequences
- Binary Golay code (Error-correcting code)
- Ternary Golay code (Error-correcting code)
References
- M.J.E. Golay (1949). "Multislit spectroscopy". J. Opt. Soc. Amer. 39: 437–444.
- M.J.E. Golay (April 1961). "Complementary series". IRE Trans. Inform. Theory IT-7: 82–87.
- M.J.E. Golay (1962). "Note on “Complementary series″". Proc. IRE 50: 84.
- R.J. Turyn (1974). "Hadamard matrices, Baumert-Hall units, four-symbol sequences, pulse compression, and surface wave encodings". J. Combin. Theory (A) 16 (3): 313–333. doi:10.1016/0097-3165(74)90056-9.
- Peter Borwein (2002). Computational excursions in probability and number theory. CMS Books in Mathematics. Springer-Verlag. pp. 110–119. ISBN 0-387-95444-9.
- P.G. Donato; J. Ureña; M. Mazo; C. De Marziani; A. Ochoa (2006). "Design and signal processing of a magnetic sensor array for train wheel detection". Sensors and actuators. A, Physical 132 (2): 516–525. doi:10.1016/j.sna.2006.02.043.